Multiple pendulum plots solutions to problems
Contents
Multiple pendulum plots solutions to problems#
Use Pendulum class to generate basic pendulum plots, applied to problems from Taylor.
Now uses a new ODE solver.
Last revised 29-Jan-2019 by Dick Furnstahl (furnstahl.1@osu.edu).
%matplotlib inline
import numpy as np
from scipy.integrate import odeint, solve_ivp
import matplotlib.pyplot as plt
# The dpi (dots-per-inch) setting will affect the resolution and how large
# the plots appear on screen and printed. So you may want/need to adjust
# the figsize when creating the figure.
plt.rcParams['figure.dpi'] = 100. # this is the default for notebook
# Change the common font size (smaller when higher dpi)
font_size = 10
plt.rcParams.update({'font.size': font_size})
Pendulum class and utility functions#
class Pendulum():
"""
Pendulum class implements the parameters and differential equation for
a pendulum using the notation from Taylor.
Parameters
----------
omega_0 : float
natural frequency of the pendulum (\sqrt{g/l} where l is the
pendulum length)
beta : float
coefficient of friction
gamma_ext : float
amplitude of external force is gamma * omega_0**2
omega_ext : float
frequency of external force
phi_ext : float
phase angle for external force
Methods
-------
dy_dt(t, y)
Returns the right side of the differential equation in vector y,
given time t and the corresponding value of y.
driving_force(t)
Returns the value of the external driving force at time t.
"""
def __init__(self, omega_0=1., beta=0.2,
gamma_ext=0.2, omega_ext=0.689, phi_ext=0.
):
self.omega_0 = omega_0
self.beta = beta
self.gamma_ext = gamma_ext
self.omega_ext = omega_ext
self.phi_ext = phi_ext
def dy_dt(self, t, y):
"""
This function returns the right-hand side of the diffeq:
[dphi/dt d^2phi/dt^2]
Parameters
----------
t : float
time
y : float
A 2-component vector with y[0] = phi(t) and y[1] = dphi/dt
Returns
-------
"""
F_ext = self.driving_force(t)
return [y[1], -self.omega_0**2 * np.sin(y[0]) - 2.*self.beta * y[1] \
+ F_ext]
def driving_force(self, t):
"""
This function returns the value of the driving force at time t.
"""
return self.gamma_ext * self.omega_0**2 \
* np.cos(self.omega_ext*t + self.phi_ext)
def solve_ode(self, t_pts, phi_0, phi_dot_0,
abserr=1.0e-8, relerr=1.0e-6):
"""
Solve the ODE given initial conditions.
For now use odeint, but we have the option to switch.
Specify smaller abserr and relerr to get more precision.
"""
y = [phi_0, phi_dot_0]
solution = solve_ivp(self.dy_dt, (t_pts[0], t_pts[-1]),
y, t_eval=t_pts,
atol=abserr, rtol=relerr)
phi, phi_dot = solution.y
return phi, phi_dot
def plot_y_vs_x(x, y, axis_labels=None, label=None, title=None,
color=None, linestyle=None, semilogy=False, loglog=False,
ax=None):
"""
Generic plotting function: return a figure axis with a plot of y vs. x,
with line color and style, title, axis labels, and line label
"""
if ax is None: # if the axis object doesn't exist, make one
ax = plt.gca()
if (semilogy):
line, = ax.semilogy(x, y, label=label,
color=color, linestyle=linestyle)
elif (loglog):
line, = ax.loglog(x, y, label=label,
color=color, linestyle=linestyle)
else:
line, = ax.plot(x, y, label=label,
color=color, linestyle=linestyle)
if label is not None: # if a label if passed, show the legend
ax.legend()
if title is not None: # set a title if one if passed
ax.set_title(title)
if axis_labels is not None: # set x-axis and y-axis labels if passed
ax.set_xlabel(axis_labels[0])
ax.set_ylabel(axis_labels[1])
return ax, line
def start_stop_indices(t_pts, plot_start, plot_stop):
start_index = (np.fabs(t_pts-plot_start)).argmin() # index in t_pts array
stop_index = (np.fabs(t_pts-plot_stop)).argmin() # index in t_pts array
return start_index, stop_index
Make plots for Taylor problem 12.8#
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 50.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.073
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# both plots: same initial conditions
phi_0 = np.pi/2
phi_dot_0 = 0.0
phi, phi_dot = p1.solve_ode(t_pts, phi_0, phi_dot_0)
# start the plot!
fig = plt.figure(figsize=(15,5))
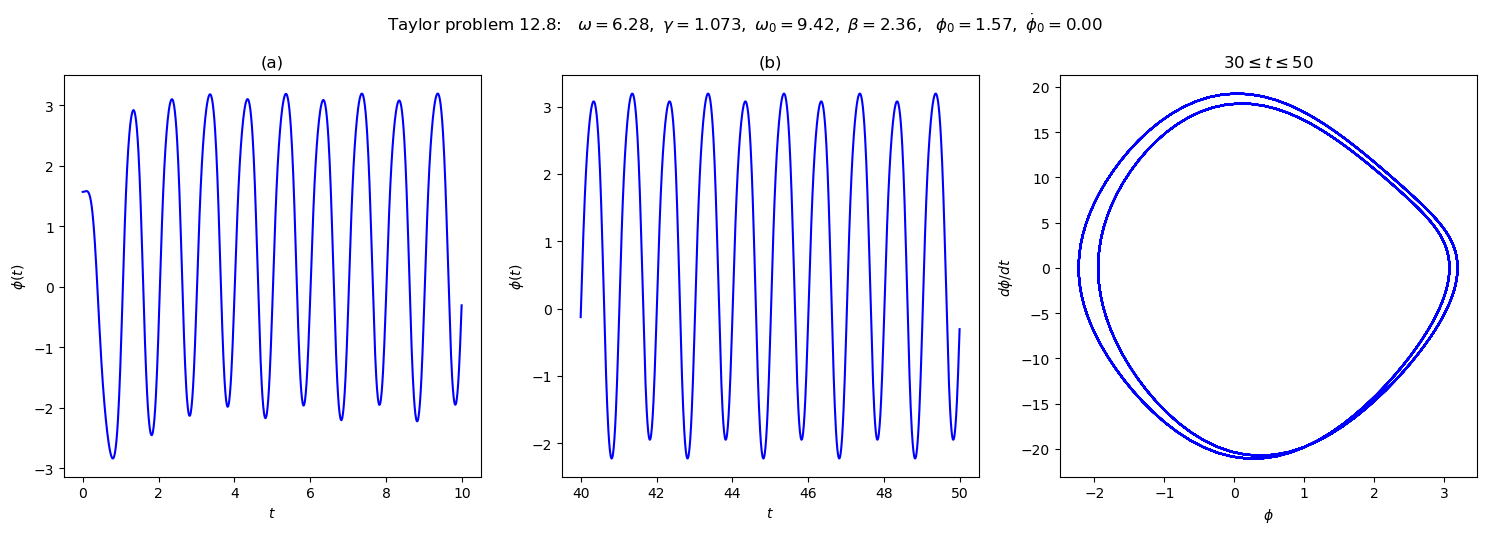
overall_title = 'Taylor problem 12.8: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f},$' + \
rf' $\phi_0 = {phi_0:.2f},$' + \
rf' $\dot\phi_0 = {phi_dot_0:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# first plot: plot from t=0 to t=10
ax_a = fig.add_subplot(1,3,1)
start, stop = start_stop_indices(t_pts, 0., 10.)
plot_y_vs_x(t_pts[start : stop], phi[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
title='(a)',
ax=ax_a)
# second plot: plot from t=40 to t=50
ax_b = fig.add_subplot(1,3,2)
start, stop = start_stop_indices(t_pts, 40., 50.)
plot_y_vs_x(t_pts[start : stop], phi[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
title='(b)',
ax=ax_b)
# third plot: state space plot from t=30 to t=50
ax_c = fig.add_subplot(1,3,3)
start, stop = start_stop_indices(t_pts, 30., 50.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$30 \leq t \leq 50$',
ax=ax_c)
fig.tight_layout()
fig.savefig('problem_12.8.png', bbox_inches='tight') # always bbox_inches='tight'
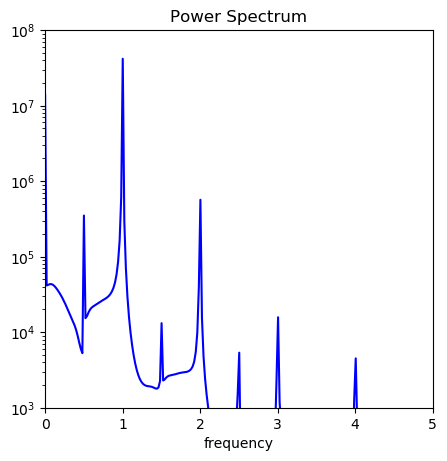
Now trying the power spectrum, plotting only positive frequencies and cutting off the lower peaks:
start, stop = start_stop_indices(t_pts, 0., t_end)
signal = phi[10:stop]
power_spectrum = np.abs(np.fft.fft(signal))**2
freqs = np.fft.fftfreq(signal.size, delta_t)
idx = np.argsort(freqs)
fig_ps = plt.figure(figsize=(5,5))
ax_ps = fig_ps.add_subplot(1,1,1)
ax_ps.semilogy(freqs[idx], power_spectrum[idx], color='blue')
ax_ps.set_xlim(0, 5.)
ax_ps.set_ylim(1.e3, 1.e8)
ax_ps.set_xlabel('frequency')
ax_ps.set_title('Power Spectrum')
Text(0.5, 1.0, 'Power Spectrum')
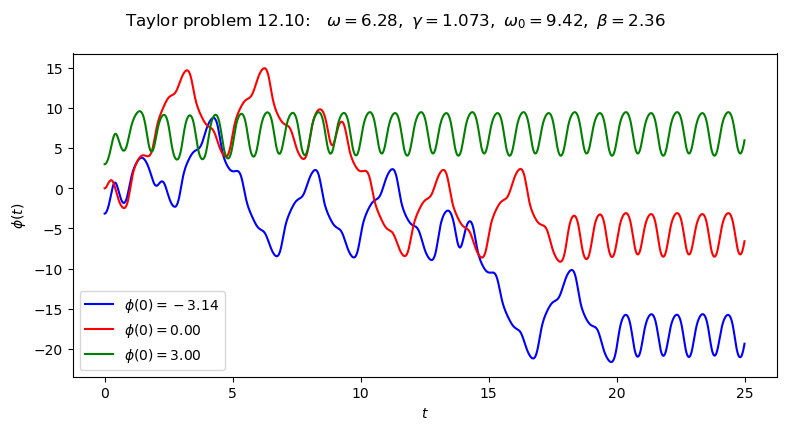
Make plots for Taylor problem 12.10#
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
delta_phi_vs_time_labels = (r'$t$', r'$|\Delta\phi(t)|$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 50.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.073
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# one plot with multiple initial conditions
phi_0_a = -np.pi
phi_dot_0 = 0.0
phi_a, phi_dot_a = p1.solve_ode(t_pts, phi_0_a, phi_dot_0,
abserr=1.e-10, relerr=1.e-10)
phi_0_b = 0.
phi_dot_0 = 0.0
phi_b, phi_dot_b = p1.solve_ode(t_pts, phi_0_b, phi_dot_0,
abserr=1.e-10, relerr=1.e-10)
phi_0_c = 3.
phi_dot_0 = 0.0
phi_c, phi_dot_c = p1.solve_ode(t_pts, phi_0_c, phi_dot_0,
abserr=1.e-10, relerr=1.e-10)
# start the plot!
fig = plt.figure(figsize=(8,4))
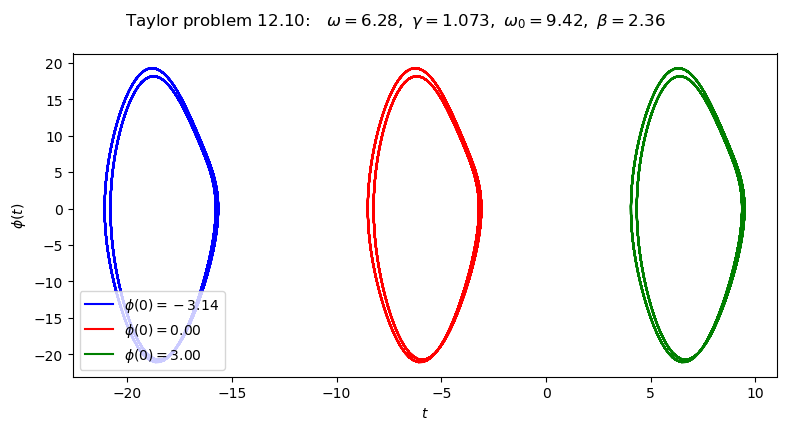
overall_title = 'Taylor problem 12.10: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# one plot: plot from t=0 to t=25
ax_a = fig.add_subplot(1,1,1)
start, stop = start_stop_indices(t_pts, 0., 25)
plot_y_vs_x(t_pts[start : stop], phi_a[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=rf'$\phi(0) = {phi_0_a:.2f}$',
ax=ax_a)
plot_y_vs_x(t_pts[start : stop], phi_b[start : stop],
axis_labels=phi_vs_time_labels,
color='red',
label=rf'$\phi(0) = {phi_0_b:.2f}$',
ax=ax_a)
plot_y_vs_x(t_pts[start : stop], phi_c[start : stop],
axis_labels=phi_vs_time_labels,
color='green',
label=rf'$\phi(0) = {phi_0_c:.2f}$',
ax=ax_a)
fig.tight_layout()
fig.savefig('problem_12.10.png', bbox_inches='tight') # always bbox_inches='tight'
# start the plot!
fig = plt.figure(figsize=(8,4))
overall_title = 'Taylor problem 12.10: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# one plot: plot from t=0 to t=25
ax_a = fig.add_subplot(1,1,1)
start, stop = start_stop_indices(t_pts, 30., 50.)
plot_y_vs_x(phi_a[start : stop], phi_dot_a[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=rf'$\phi(0) = {phi_0_a:.2f}$',
ax=ax_a)
plot_y_vs_x(phi_b[start : stop], phi_dot_b[start : stop],
axis_labels=phi_vs_time_labels,
color='red',
label=rf'$\phi(0) = {phi_0_b:.2f}$',
ax=ax_a)
plot_y_vs_x(phi_c[start : stop], phi_dot_c[start : stop],
axis_labels=phi_vs_time_labels,
color='green',
label=rf'$\phi(0) = {phi_0_c:.2f}$',
ax=ax_a)
fig.tight_layout()
fig.savefig('problem_12.10_alt.png', bbox_inches='tight')
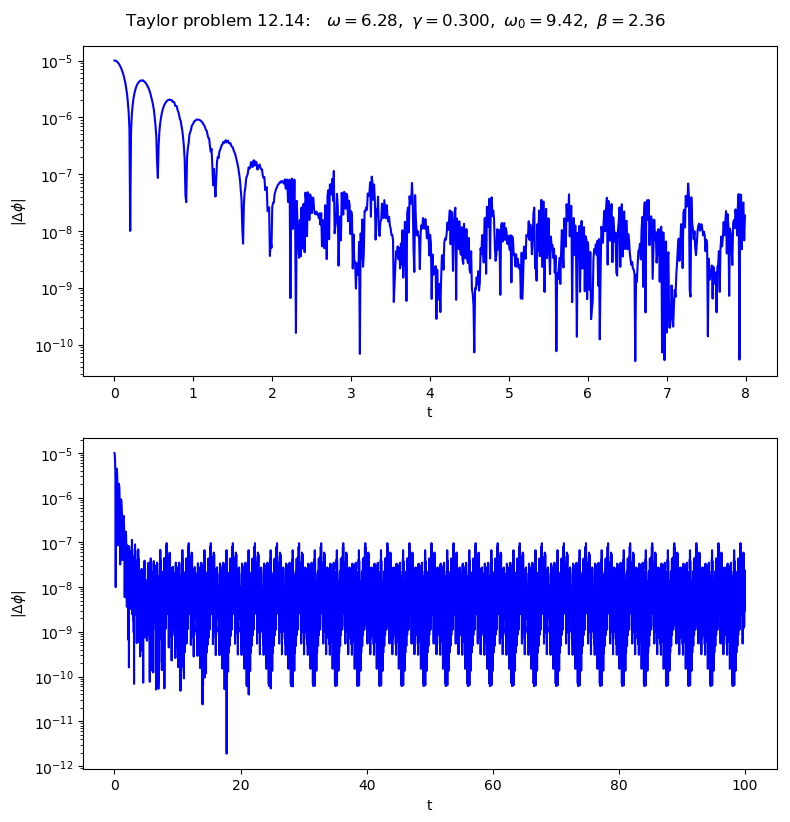
Make plots for Taylor problem 12.14#
This time we plot \(\Delta \phi\).
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
Delta_phi_vs_time_labels = (r'$t$', r'$\Delta\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 100.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.084
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# one plot with multiple initial conditions
phi_0_1 = 0.0
phi_dot_0 = 0.0
phi_1, phi_dot_1 = p1.solve_ode(t_pts, phi_0_1, phi_dot_0)
phi_0_2 = 0.00001
phi_dot_0 = 0.0
phi_2, phi_dot_2 = p1.solve_ode(t_pts, phi_0_2, phi_dot_0)
# Calculate the absolute value of \phi_2 - \phi_1
Delta_phi = np.fabs(phi_2 - phi_1)
# start the plot!
fig = plt.figure(figsize=(8,8))
overall_title = 'Taylor problem 12.14: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# two plot: plot from t=0 to t=8 and another from t=0 to t=100
ax_a = fig.add_subplot(2,1,1)
start, stop = start_stop_indices(t_pts, 0., 8.)
ax_a.semilogy(t_pts[start : stop], Delta_phi[start : stop],
color='blue', label=None)
ax_a.set_xlabel('t')
ax_a.set_ylabel(r'$|\Delta\phi|$')
ax_b = fig.add_subplot(2,1,2)
start, stop = start_stop_indices(t_pts, 0., 100.)
plot_y_vs_x(t_pts[start : stop], Delta_phi[start : stop],
color='blue', label=None, semilogy=True)
ax_b.set_xlabel('t')
ax_b.set_ylabel(r'$|\Delta\phi|$')
fig.tight_layout()
# always bbox_inches='tight' for best results. Further adjustments also.
fig.savefig('problem_12.14.png', bbox_inches='tight')
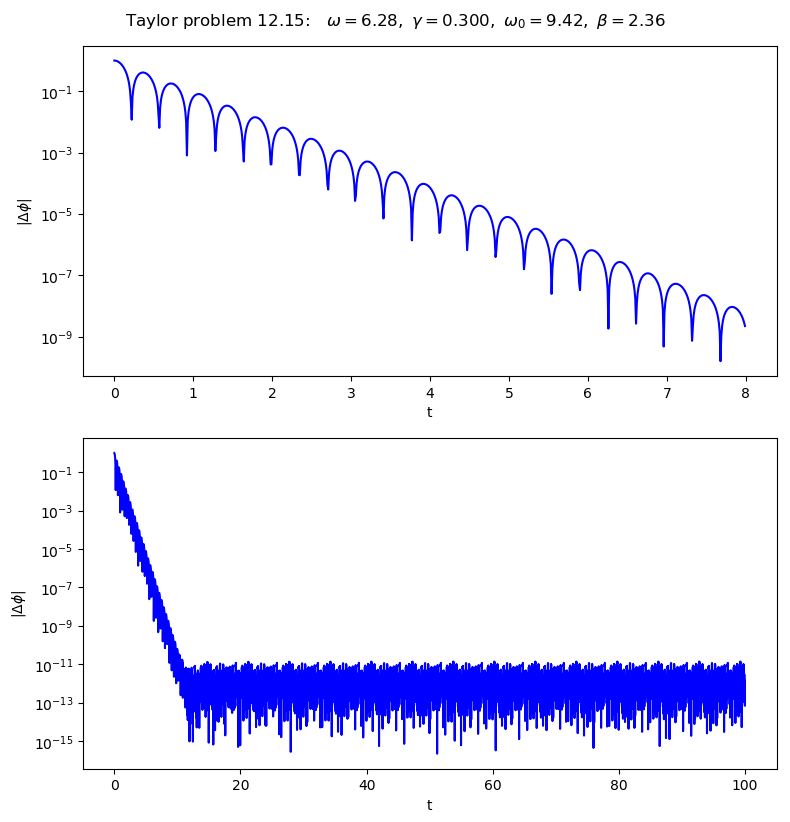
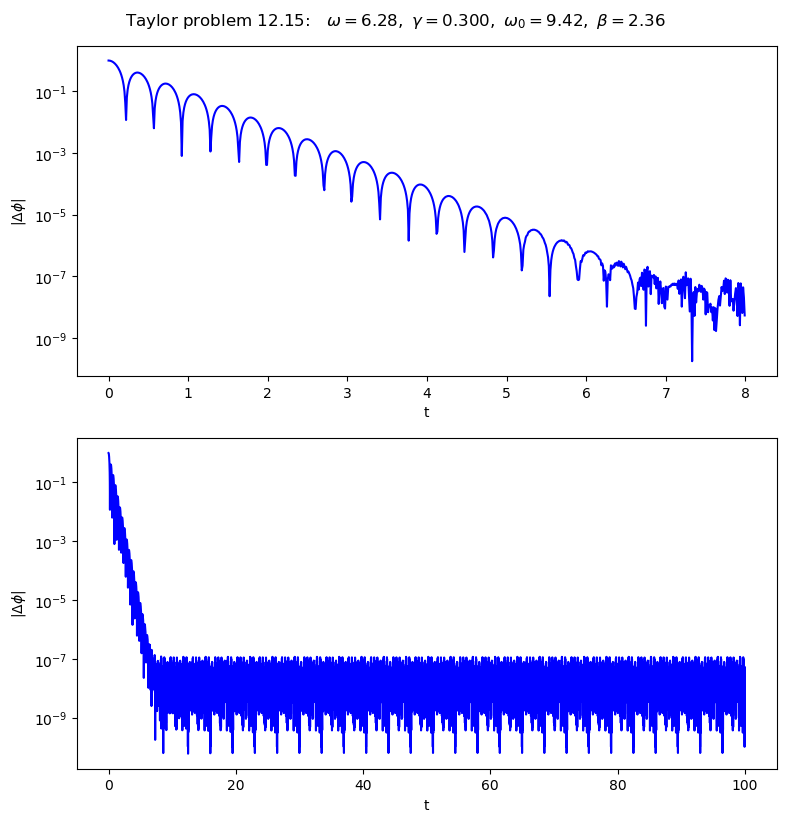
Make plots for Taylor problem 12.15#
This time we plot \(\Delta \phi\).
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
Delta_phi_vs_time_labels = (r'$t$', r'$\Delta\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 100.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 0.3
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# one plot with multiple initial conditions
phi_0_1 = 0.0
phi_dot_0 = 0.0
phi_1, phi_dot_1 = p1.solve_ode(t_pts, phi_0_1, phi_dot_0)
phi_0_2 = 1.0
phi_dot_0 = 0.0
phi_2, phi_dot_2 = p1.solve_ode(t_pts, phi_0_2, phi_dot_0)
# Calculate the absolute value of \phi_2 - \phi_1
Delta_phi = np.fabs(phi_2 - phi_1)
# start the plot!
fig = plt.figure(figsize=(8,8))
overall_title = 'Taylor problem 12.15: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# two plot: plot from t=0 to t=8 and another from t=0 to t=100
ax_a = fig.add_subplot(2,1,1)
start, stop = start_stop_indices(t_pts, 0., 8.)
ax_a.semilogy(t_pts[start : stop], Delta_phi[start : stop],
color='blue', label=None)
ax_a.set_xlabel('t')
ax_a.set_ylabel(r'$|\Delta\phi|$')
ax_b = fig.add_subplot(2,1,2)
start, stop = start_stop_indices(t_pts, 0., 100.)
plot_y_vs_x(t_pts[start : stop], Delta_phi[start : stop],
color='blue', label=None, semilogy=True)
ax_b.set_xlabel('t')
ax_b.set_ylabel(r'$|\Delta\phi|$')
fig.tight_layout()
# always bbox_inches='tight' for best results. Further adjustments also.
fig.savefig('problem_12.15.png', bbox_inches='tight')
Now repeat with smaller abserr and relerr for the ode solver:
# one plot with multiple initial conditions
phi_0_1 = 0.0
phi_dot_0 = 0.0
phi_1, phi_dot_1 = p1.solve_ode(t_pts, phi_0_1, phi_dot_0,
abserr=1.e-10, relerr=1.e-10)
phi_0_2 = 1.0
phi_dot_0 = 0.0
phi_2, phi_dot_2 = p1.solve_ode(t_pts, phi_0_2, phi_dot_0,
abserr=1.e-10, relerr=1.e-10)
# Calculate the absolute value of \phi_2 - \phi_1
Delta_phi = np.fabs(phi_2 - phi_1)
# start the plot!
fig = plt.figure(figsize=(8,8))
overall_title = 'Taylor problem 12.15: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# two plot: plot from t=0 to t=8 and another from t=0 to t=100
ax_a = fig.add_subplot(2,1,1)
start, stop = start_stop_indices(t_pts, 0., 8.)
ax_a.semilogy(t_pts[start : stop], Delta_phi[start : stop],
color='blue', label=None)
ax_a.set_xlabel('t')
ax_a.set_ylabel(r'$|\Delta\phi|$')
ax_b = fig.add_subplot(2,1,2)
start, stop = start_stop_indices(t_pts, 0., 100.)
plot_y_vs_x(t_pts[start : stop], Delta_phi[start : stop],
color='blue', label=None, semilogy=True)
ax_b.set_xlabel('t')
ax_b.set_ylabel(r'$|\Delta\phi|$')
fig.tight_layout()
# always bbox_inches='tight' for best results. Further adjustments also.
fig.savefig('problem_12.15.png', bbox_inches='tight')