Brachistochrone problem (static)#

Adapted from https://scipython.com/blog/the-brachistochrone-problem/.

We assume that the curve starts at \((x_1, y_1) = (0, 0)\) and use the solution for the cycloid:

\(\begin{align} x &= a (\theta - \sin\theta) \\ y &= a (1 - \cos\theta) \;. \end{align}\)

We want to be solve the problem with a specified final point \((x_2, y_2)\), which means finding \(a\) and \(\theta_2\) (note that \(\theta_1 = 0\)). We can find \(\theta_2\) from the ratio:

\(\begin{align} \frac{y_2}{x_2} = \frac{1 - \cos\theta_2}{\theta_2 - \sin\theta_2} \, \end{align}\)

which we solve numerically by finding where the difference of the two sides is zero as a function of \(\theta_2\). We use the scipy.integrate function newton, which implements the Newton-Raphson method for finding roots of an equation.

With \(\theta_2\) known, \(a\) is given by

\(\begin{align} a = \frac{y_2}{1 - \cos\theta_2} \;. \end{align}\)

For alternative paths, we consider a circle, a parabola, and a straight line. The functional for the time to be minimized is:

\(\begin{align} \mbox{time}(1\rightarrow 2) = \frac{1}{\sqrt{2g}} \int_{0}^{x_2} \frac{\sqrt{1 + y'(x)^2}}{\sqrt{y(x)}} dx \;, \end{align}\)

which is written with \(y(x)\) and \(dx\) (i.e., an integral over \(x\)) rather than \(x(y)\) and \(dy\) as in Taylor. (We still measure positive \(y\) to be downward from the origin, in the same direction as gravity.)

We evaluate the functional numerically in all cases, even when we could do it algebraically.

import numpy as np
import matplotlib.pyplot as plt

from scipy.optimize import newton
from scipy.integrate import quad

%matplotlib inline

def functional(x, f, df_dx):
    """The integrand of the time integral to be minimized for a path f(x)."""

    return np.sqrt((1. + df_dx(x)**2) / (2 * g * f(x)))


def cycloid(x_2, y_2, N=100):
    """Return the path of Brachistochrone curve from (0, 0) to (x_2, y_2).

    The Brachistochrone curve is the path down which a bead will slide without
    friction between two points in the least time (an arc of a cycloid).
    Returned as an array of N values of (x, y) between (0, 0) and (x_2, y_2).

    Solves for the value of theta_2 to correspond to (x_2, y_2), assuming
    it starts from the origin, from the given ratio of y_2/x_2, which should
    equal 
    """

    # First find theta_2 from (x_2, y_2) numerically (by Newton-Rapheson).
    def find_theta(theta):
        """Equation that will be zero for theta=theta_2 with 
            (x, y) = (x_2, y_2)."""
        return y_2/x_2 - (1. - np.cos(theta))/(theta - np.sin(theta))
    theta_2 = newton(find_theta, np.pi/2.)  # Second argument is first guess.

    # The radius of the circle generating the cycloid
    a = y_2 / (1. - np.cos(theta_2))

    # Set up array of x and y points from the origin to (x_2, y_2)
    theta_1 = 0.
    theta_pts = np.linspace(theta_1, theta_2, N)
    x_pts = a * (theta_pts - np.sin(theta_pts))
    y_pts = a * (1. - np.cos(theta_pts))

    # The time of travel
    T = theta_2 * np.sqrt(a / g)
    print(f'T(cycloid) = {T:.3f}')
    return x_pts, y_pts, T


def parabola(x_2, y_2, N=100):
    """Return the path of a parabolic arc between (0,0) to (x_2, y_2).

    The parabola used is the one with a vertical tangent at (0,0).

    """

    c = y_2**2/x_2

    def f_parabola(x):
        """Equation of a parabola going through the origin and (x_2, y_2)."""
        return np.sqrt(c*x)
    def df_parabola_dx(x):
        return c/2/f_parabola(x)

    x_pts = np.linspace(0, x_2, N)
    y_pts = f_parabola(x_pts)

    # Calculate the time of travel by numerical integration.
    T, T_error = quad(functional, 0., x_2, args=(f_parabola, df_parabola_dx))
    print(f'T(parabola) = {T:.3f}')
    return x_pts, y_pts, T


def circle(x_2, y_2, N=100):
    """Return the path of a circular arc between (0,0) to (x_2, y_2).

    The circle used is the one with a vertical tangent at (0,0).

    """

    # Circle radius
    ### r = 

    ###def f_circle(x):
        ### return 
    ###def df_circle_dx(x):
        ###return (r-x)/f_circle(x)

    x_pts = np.linspace(0, x_2, N)
    y_pts = f_circle(x_pts)

    # Calculate the time of travel by numerical integration.
    ###T, T_error = 
    ###print(f'T(circle) = {T:.3f}')
    return x_pts, y_pts, T


###def linear(x_2, y_2, N=100):
    ### """Return the path of a straight line from (0,0) to (x_2, y_2)."""

    ### m = =
    ### x_pts = 
    ### y_pts = 

    ### def f_linear(x):
        ### return 
    ### def df_linear_dx(x):
        ### return 

    # Calculate time of travel
    ### T_exact = 
    ### T, T_error = 

    ### print(f'T(linear) = {T:.3f}, (exact = {T_exact:.3f})')
    ### return x_pts, y_pts, T

# Acceleration due to gravity (mks units); final position of bead (m).
g = 9.81
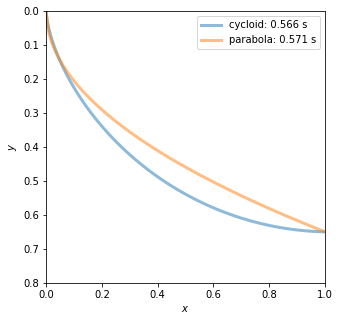
x_2, y_2 = 1., 0.65

# Plot a figure comparing the four paths.
fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(1,1,1)

### for curve in ('cycloid', 'parabola', 'circle', 'linear'):
for curve in ('cycloid', 'parabola'):
    x, y, T = globals()[curve](x_2, y_2)
    ax.plot(x, y, lw=3, alpha=0.5, label=f'{curve}: {T:.3f} s')
ax.legend()

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_xlim(0, x_2)
ax.set_ylim(0.8, 0)
plt.savefig('brachistochrone_homework.png')
plt.show()

T(cycloid) = 0.566
T(parabola) = 0.571
../../_images/Brachistochrone_static_homework_5_1.png