Multiple pendulum plots. Section 12.4: Approach to Chaos
Contents
Multiple pendulum plots. Section 12.4: Approach to Chaos#
Use Pendulum class to generate basic pendulum plots. Applied here to figures from Taylor Section 12.4.
Last revised 23-Jan-2019 by Dick Furnstahl (furnstahl.1@osu.edu).
%matplotlib inline
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
Pendulum class and utility functions#
class Pendulum():
"""
Pendulum class implements the parameters and differential equation for
a pendulum using the notation from Taylor.
Parameters
----------
omega_0 : float
natural frequency of the pendulum (\sqrt{g/l} where l is the
pendulum length)
beta : float
coefficient of friction
gamma_ext : float
amplitude of external force is gamma * omega_0**2
omega_ext : float
frequency of external force
phi_ext : float
phase angle for external force
Methods
-------
dy_dt(y, t)
Returns the right side of the differential equation in vector y,
given time t and the corresponding value of y.
driving_force(t)
Returns the value of the external driving force at time t.
"""
def __init__(self, omega_0=1., beta=0.2,
gamma_ext=0.2, omega_ext=0.689, phi_ext=0.
):
self.omega_0 = omega_0
self.beta = beta
self.gamma_ext = gamma_ext
self.omega_ext = omega_ext
self.phi_ext = phi_ext
def dy_dt(self, y, t):
"""
This function returns the right-hand side of the diffeq:
[dphi/dt d^2phi/dt^2]
Parameters
----------
y : float
A 2-component vector with y[0] = phi(t) and y[1] = dphi/dt
t : float
time
Returns
-------
"""
F_ext = self.driving_force(t)
return [y[1], -self.omega_0**2 * np.sin(y[0]) - 2.*self.beta * y[1] \
+ F_ext]
def driving_force(self, t):
"""
This function returns the value of the driving force at time t.
"""
return self.gamma_ext * self.omega_0**2 \
* np.cos(self.omega_ext*t + self.phi_ext)
def solve_ode(self, phi_0, phi_dot_0, abserr=1.0e-8, relerr=1.0e-6):
"""
Solve the ODE given initial conditions.
For now use odeint, but we have the option to switch.
Specify smaller abserr and relerr to get more precision.
"""
y = [phi_0, phi_dot_0]
phi, phi_dot = odeint(self.dy_dt, y, t_pts,
atol=abserr, rtol=relerr).T
return phi, phi_dot
def plot_y_vs_x(x, y, axis_labels=None, label=None, title=None,
color=None, linestyle=None, semilogy=False, loglog=False,
ax=None):
"""
Generic plotting function: return a figure axis with a plot of y vs. x,
with line color and style, title, axis labels, and line label
"""
if ax is None: # if the axis object doesn't exist, make one
ax = plt.gca()
if (semilogy):
line, = ax.semilogy(x, y, label=label,
color=color, linestyle=linestyle)
elif (loglog):
line, = ax.loglog(x, y, label=label,
color=color, linestyle=linestyle)
else:
line, = ax.plot(x, y, label=label,
color=color, linestyle=linestyle)
if label is not None: # if a label if passed, show the legend
ax.legend()
if title is not None: # set a title if one if passed
ax.set_title(title)
if axis_labels is not None: # set x-axis and y-axis labels if passed
ax.set_xlabel(axis_labels[0])
ax.set_ylabel(axis_labels[1])
return ax, line
def start_stop_indices(t_pts, plot_start, plot_stop):
"""Given an array (e.g., of times) and desired starting and stop values,
return the array indices that are closest to those values.
"""
start_index = (np.fabs(t_pts-plot_start)).argmin() # index in t_pts array
stop_index = (np.fabs(t_pts-plot_stop)).argmin() # index in t_pts array
return start_index, stop_index
Make plots for Taylor Figure 12.4#
We’ll set it up with the specified parameters.
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 100.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.06
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# initial conditions specified
phi_0 = 0.
phi_dot_0 = 0.0
phi, phi_dot = p1.solve_ode(phi_0, phi_dot_0)
# Change the common font size
font_size = 14
plt.rcParams.update({'font.size': font_size})
# start the plot!
fig = plt.figure(figsize=(15,5))
overall_title = 'Taylor Figure 12.4: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f},$' + \
rf' $\phi_0 = {phi_0:.2f},$' + \
rf' $\dot\phi_0 = {phi_dot_0:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# first plot: plot from t=0 to t=15
ax_a = fig.add_subplot(1,3,1)
start, stop = start_stop_indices(t_pts, 0., 15.)
plot_y_vs_x(t_pts[start : stop], phi[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
title='Figure 12.4',
ax=ax_a)
# second plot: state space plot from t=0 to t=15
ax_b = fig.add_subplot(1,3,2)
start, stop = start_stop_indices(t_pts, 0., 15.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$0 \leq t \leq 15$',
ax=ax_b)
# third plot: state space plot from t= to t=12
ax_c = fig.add_subplot(1,3,3)
start, stop = start_stop_indices(t_pts, 10., 30.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$10 \leq t \leq 30$',
ax=ax_c)
fig.tight_layout()
fig.savefig('Figure_12.4.png', bbox_inches='tight') # always bbox_inches='tight'
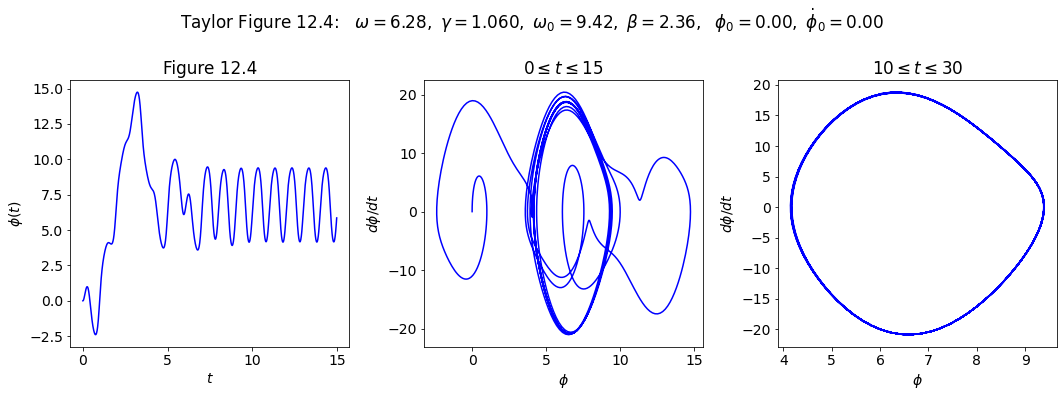
Let’s check for periodicity after the transients die out. Print out phi(t) once every period of the external driving force.
# First pass at periodicity check
start, stop = start_stop_indices(t_pts, 50., 70.)
tau_ext = 2.*np.pi / omega_ext
delta_index = int(tau_ext / delta_t)
print(' t phi(t)')
for index in range(start, stop, delta_index):
print(f' {t_pts[index]:.1f} {phi[index]:.4f}')
t phi(t)
50.0 6.0366
51.0 6.0366
52.0 6.0366
53.0 6.0367
54.0 6.0366
55.0 6.0367
56.0 6.0366
57.0 6.0366
58.0 6.0366
59.0 6.0366
60.0 6.0366
61.0 6.0366
62.0 6.0366
63.0 6.0366
64.0 6.0366
65.0 6.0366
66.0 6.0366
67.0 6.0366
68.0 6.0366
69.0 6.0366
Now trying the power spectrum in steady state, plotting only positive frequencies and cutting off any lower peaks from noise. We multiply the frequencies by \(2\pi\) to get the angular frequency. What do you observe?
start, stop = start_stop_indices(t_pts, 20., t_end)
signal = phi[start:stop]
power_spectrum = np.abs(np.fft.fft(signal))**2
freqs = 2.*np.pi * np.fft.fftfreq(signal.size, delta_t)
idx = np.argsort(freqs)
fig_ps = plt.figure(figsize=(5,5))
ax_ps = fig_ps.add_subplot(1,1,1)
ax_ps.semilogy(freqs[idx], power_spectrum[idx], color='blue')
ax_ps.set_xlim(0, 30.)
ax_ps.set_ylim(1.e4, 1.e9)
ax_ps.set_xlabel('frequency (Hz)')
ax_ps.set_title('Power Spectrum for Figure 12.4')
fig_ps.tight_layout()
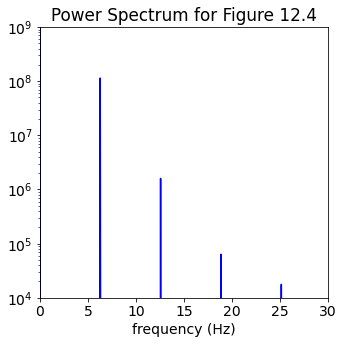
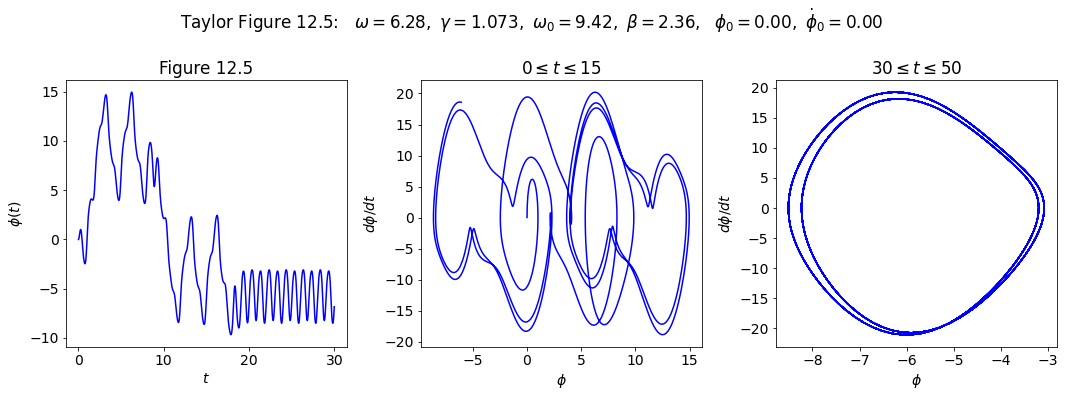
Figure 12.5: Pick conditions and then analyze#
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 100.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.073
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# initial conditions specified
phi_0 = 0.
phi_dot_0 = 0.0
phi, phi_dot = p1.solve_ode(phi_0, phi_dot_0)
# Change the common font size
font_size = 14
plt.rcParams.update({'font.size': font_size})
# start the plot!
fig = plt.figure(figsize=(15,5))
overall_title = 'Taylor Figure 12.5: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f},$' + \
rf' $\phi_0 = {phi_0:.2f},$' + \
rf' $\dot\phi_0 = {phi_dot_0:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# first plot: plot from t=0 to t=15
ax_a = fig.add_subplot(1,3,1)
start, stop = start_stop_indices(t_pts, 0., 30.)
plot_y_vs_x(t_pts[start : stop], phi[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
title='Figure 12.5',
ax=ax_a)
# second plot: state space plot from t=0 to t=15
ax_b = fig.add_subplot(1,3,2)
start, stop = start_stop_indices(t_pts, 0., 15.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$0 \leq t \leq 15$',
ax=ax_b)
# third plot: state space plot from t= to t=12
ax_c = fig.add_subplot(1,3,3)
start, stop = start_stop_indices(t_pts, 30., 50.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$30 \leq t \leq 50$',
ax=ax_c)
fig.tight_layout()
fig.savefig('Figure_12.5.png', bbox_inches='tight') # always bbox_inches='tight'
# First pass at periodicity check
start, stop = start_stop_indices(t_pts, 50., 70.)
tau_ext = 2.*np.pi / omega_ext
delta_index = int(tau_ext / delta_t)
print(' t phi(t)')
for index in range(start, stop, delta_index):
print(f' {t_pts[index]:.1f} {phi[index]:.4f}')
t phi(t)
50.0 -6.6438
51.0 -6.4090
52.0 -6.6438
53.0 -6.4090
54.0 -6.6438
55.0 -6.4090
56.0 -6.6439
57.0 -6.4090
58.0 -6.6437
59.0 -6.4090
60.0 -6.6438
61.0 -6.4090
62.0 -6.6437
63.0 -6.4090
64.0 -6.6438
65.0 -6.4090
66.0 -6.6438
67.0 -6.4090
68.0 -6.6438
69.0 -6.4090
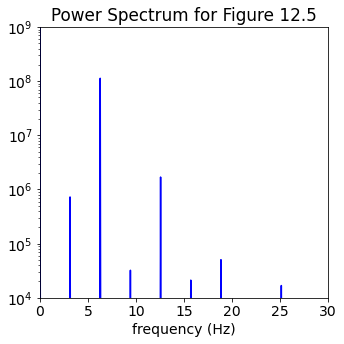
Now trying the power spectrum in steady state, plotting only positive frequencies and cutting off any lower peaks from noise. We multiply the frequencies by \(2\pi\) to get the angular frequency. What do you observe?
start, stop = start_stop_indices(t_pts, 20., t_end)
signal = phi[start:stop]
power_spectrum = np.abs(np.fft.fft(signal))**2
freqs = 2.*np.pi * np.fft.fftfreq(signal.size, delta_t)
idx = np.argsort(freqs)
fig_ps = plt.figure(figsize=(5,5))
ax_ps = fig_ps.add_subplot(1,1,1)
ax_ps.semilogy(freqs[idx], power_spectrum[idx], color='blue')
ax_ps.set_xlim(0, 30.)
ax_ps.set_ylim(1.e4, 1.e9)
ax_ps.set_xlabel('frequency (Hz)')
ax_ps.set_title('Power Spectrum for Figure 12.5')
fig_ps.tight_layout()
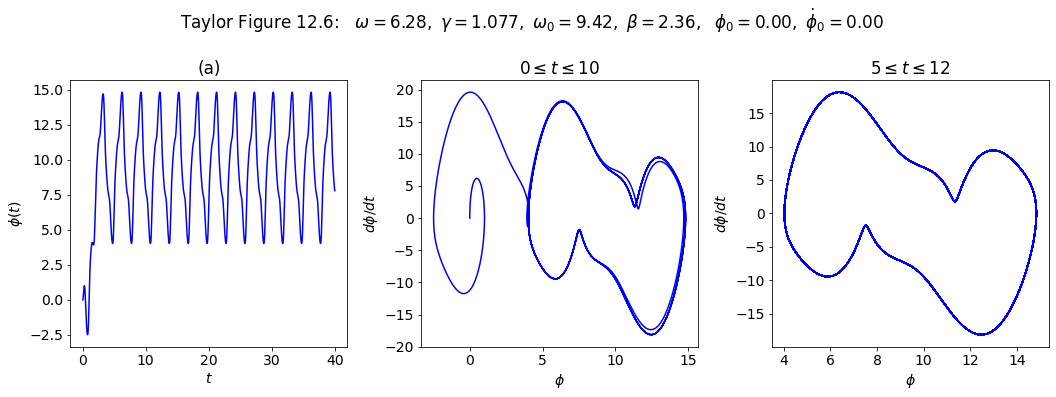
Make plots for Taylor Figure 12.6#
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 100.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.077
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# initial conditions specified
phi_0 = 0.
phi_dot_0 = 0.0
phi, phi_dot = p1.solve_ode(phi_0, phi_dot_0)
phi_fig12_6 = phi
# Change the common font size
font_size = 14
plt.rcParams.update({'font.size': font_size})
# start the plot!
fig = plt.figure(figsize=(15,5))
overall_title = 'Taylor Figure 12.6: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f},$' + \
rf' $\phi_0 = {phi_0:.2f},$' + \
rf' $\dot\phi_0 = {phi_dot_0:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# first plot: plot from t=0 to t=10
ax_a = fig.add_subplot(1,3,1)
start, stop = start_stop_indices(t_pts, 0., 40.)
plot_y_vs_x(t_pts[start : stop], phi[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
title='(a)',
ax=ax_a)
# second plot: state space plot from t=0 to t=10
ax_b = fig.add_subplot(1,3,2)
start, stop = start_stop_indices(t_pts, 0., 15.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$0 \leq t \leq 10$',
ax=ax_b)
# third plot: state space plot from t=5 to t=12
ax_c = fig.add_subplot(1,3,3)
start, stop = start_stop_indices(t_pts, 20, 100.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$5 \leq t \leq 12$',
ax=ax_c)
fig.tight_layout()
fig.savefig('Figure_12.6.png', bbox_inches='tight') # always bbox_inches='tight'
# First pass at periodicity check
start, stop = start_stop_indices(t_pts, 50., 70.)
tau_ext = 2.*np.pi / omega_ext
delta_index = int(tau_ext / delta_t)
print(' t phi(t)')
for index in range(start, stop, delta_index):
print(f' {t_pts[index]:.1f} {phi[index]:.4f}')
t phi(t)
50.0 6.8727
51.0 13.8122
52.0 7.7585
53.0 6.8727
54.0 13.8122
55.0 7.7585
56.0 6.8727
57.0 13.8123
58.0 7.7585
59.0 6.8727
60.0 13.8122
61.0 7.7585
62.0 6.8727
63.0 13.8122
64.0 7.7585
65.0 6.8727
66.0 13.8122
67.0 7.7585
68.0 6.8726
69.0 13.8123
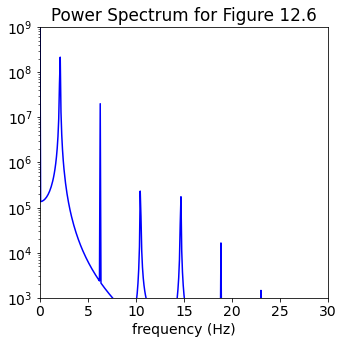
Now trying the power spectrum in steady state, plotting only positive frequencies and cutting off any lower peaks from noise. We multiply the frequencies by \(2\pi\) to get the angular frequency. What do you observe?
start, stop = start_stop_indices(t_pts, 20., t_end)
signal = phi[start:stop]
power_spectrum = np.abs(np.fft.fft(signal))**2
freqs = 2.*np.pi * np.fft.fftfreq(signal.size, delta_t)
idx = np.argsort(freqs)
fig_ps = plt.figure(figsize=(5,5))
ax_ps = fig_ps.add_subplot(1,1,1)
ax_ps.semilogy(freqs[idx], power_spectrum[idx], color='blue')
ax_ps.set_xlim(0, 30.)
ax_ps.set_ylim(1.e3, 1.e9)
ax_ps.set_xlabel('frequency (Hz)')
ax_ps.set_title('Power Spectrum for Figure 12.6')
fig_ps.tight_layout()
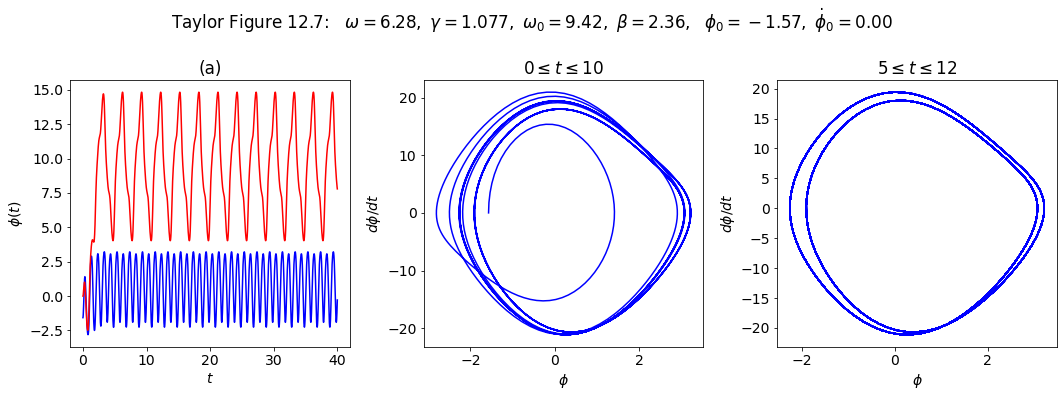
Make plots for Taylor Figure 12.7#
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 500.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common pendulum parameters
gamma_ext = 1.077
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate a pendulum
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts
driving = p1.driving_force(t_pts)
# initial conditions specified
phi_0 = -np.pi/2.
phi_dot_0 = 0.0
phi, phi_dot = p1.solve_ode(phi_0, phi_dot_0)
# Change the common font size
font_size = 14
plt.rcParams.update({'font.size': font_size})
# start the plot!
fig = plt.figure(figsize=(15,5))
overall_title = 'Taylor Figure 12.7: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\gamma = {gamma_ext:.3f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f},$' + \
rf' $\phi_0 = {phi_0:.2f},$' + \
rf' $\dot\phi_0 = {phi_dot_0:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# first plot: plot from t=0 to t=10
ax_a = fig.add_subplot(1,3,1)
start, stop = start_stop_indices(t_pts, 0., 40.)
plot_y_vs_x(t_pts[start : stop], phi[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
title='(a)',
ax=ax_a)
plot_y_vs_x(t_pts[start : stop], phi_fig12_6[start : stop],
axis_labels=phi_vs_time_labels,
color='red',
label=None,
ax=ax_a)
# second plot: state space plot from t=0 to t=15
ax_b = fig.add_subplot(1,3,2)
start, stop = start_stop_indices(t_pts, 0., 15.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$0 \leq t \leq 10$',
ax=ax_b)
# third plot: state space plot from t=5 to t=12
ax_c = fig.add_subplot(1,3,3)
start, stop = start_stop_indices(t_pts, 20, 100.)
plot_y_vs_x(phi[start : stop], phi_dot[start : stop],
axis_labels=state_space_labels,
color='blue',
label=None,
title=rf'$5 \leq t \leq 12$',
ax=ax_c)
fig.tight_layout()
fig.savefig('Figure_12.7.png', bbox_inches='tight') # always bbox_inches='tight'
# First pass at periodicity check
start, stop = start_stop_indices(t_pts, 50., 70.)
tau_ext = 2.*np.pi / omega_ext
delta_index = int(tau_ext / delta_t)
print(' t phi(t)')
for index in range(start, stop, delta_index):
print(f' {t_pts[index]:.1f} {phi[index]:.4f}')
t phi(t)
50.0 -0.1071
51.0 -0.4051
52.0 -0.1071
53.0 -0.4050
54.0 -0.1071
55.0 -0.4050
56.0 -0.1071
57.0 -0.4050
58.0 -0.1071
59.0 -0.4051
60.0 -0.1071
61.0 -0.4049
62.0 -0.1070
63.0 -0.4051
64.0 -0.1071
65.0 -0.4050
66.0 -0.1071
67.0 -0.4050
68.0 -0.1071
69.0 -0.4050
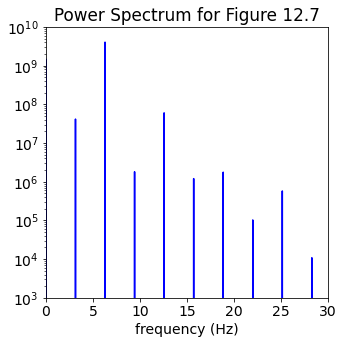
Now trying the power spectrum in steady state, plotting only positive frequencies and cutting off any lower peaks from noise. We multiply the frequencies by \(2\pi\) to get the angular frequency. What do you observe?
start, stop = start_stop_indices(t_pts, 20., t_end)
signal = phi[start:stop]
power_spectrum = np.abs(np.fft.fft(signal))**2
freqs = 2.*np.pi * np.fft.fftfreq(signal.size, delta_t)
idx = np.argsort(freqs)
fig_ps = plt.figure(figsize=(5,5))
ax_ps = fig_ps.add_subplot(1,1,1)
ax_ps.semilogy(freqs[idx], power_spectrum[idx], color='blue')
ax_ps.set_xlim(0, 30.)
ax_ps.set_ylim(1.e3, 1.e10)
ax_ps.set_xlabel('frequency (Hz)')
ax_ps.set_title('Power Spectrum for Figure 12.7')
fig_ps.tight_layout()
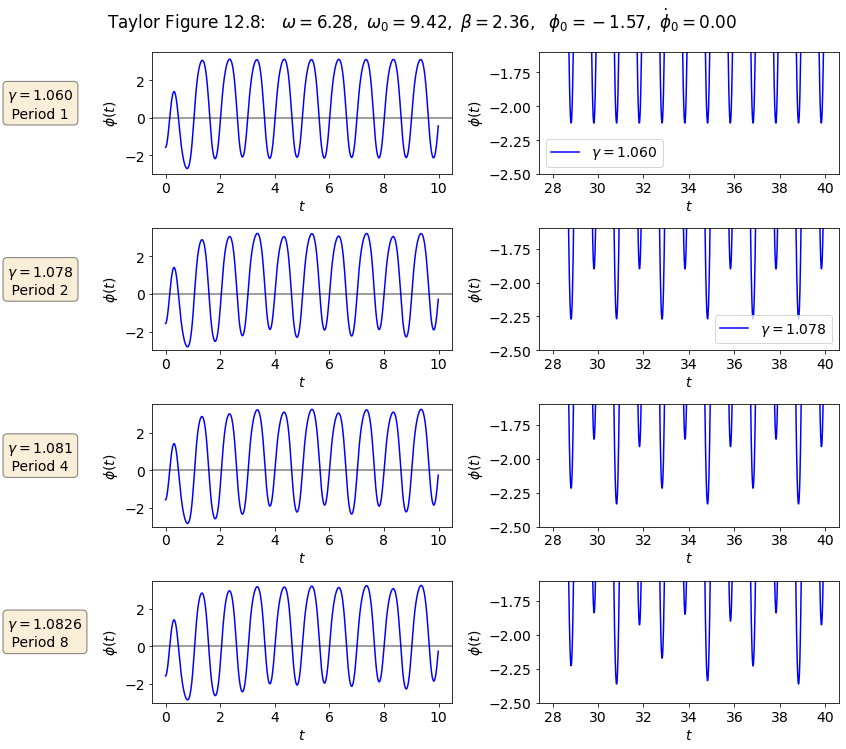
Make plots for Taylor Figure 12.8#
Now we try to plot a period doubling cascade as in Figure 12.8. This will mean plots of four different conditions, each with two plots.
# Labels for individual plot axes
phi_vs_time_labels = (r'$t$', r'$\phi(t)$')
phi_dot_vs_time_labels = (r'$t$', r'$d\phi/dt(t)$')
state_space_labels = (r'$\phi$', r'$d\phi/dt$')
# Common plotting time (generate the full time then use slices)
t_start = 0.
t_end = 100.
delta_t = 0.01
t_pts = np.arange(t_start, t_end+delta_t, delta_t)
# Common parameters
omega_ext = 2.*np.pi
phi_ext = 0.
omega_0 = 1.5*omega_ext
beta = omega_0/4.
# Instantiate the pendulu s
gamma_ext = 1.060
p1 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
gamma_ext = 1.078
p2 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
gamma_ext = 1.081
p3 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
gamma_ext = 1.0826
p4 = Pendulum(omega_0=omega_0, beta=beta,
gamma_ext=gamma_ext, omega_ext=omega_ext, phi_ext=phi_ext)
# calculate the driving force for t_pts (all the same)
driving = p1.driving_force(t_pts)
# same initial conditions specified
phi_0 = -np.pi / 2.
phi_dot_0 = 0.
# solve each of the pendulum odes
phi_1, phi_dot_1 = p1.solve_ode(phi_0, phi_dot_0)
phi_2, phi_dot_2 = p2.solve_ode(phi_0, phi_dot_0)
phi_3, phi_dot_3 = p3.solve_ode(phi_0, phi_dot_0)
phi_4, phi_dot_4 = p4.solve_ode(phi_0, phi_dot_0)
# Change the common font size
font_size = 14
plt.rcParams.update({'font.size': font_size})
box_props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
# start the plot!
fig = plt.figure(figsize=(12,10))
overall_title = 'Taylor Figure 12.8: ' + \
rf' $\omega = {omega_ext:.2f},$' + \
rf' $\omega_0 = {omega_0:.2f},$' + \
rf' $\beta = {beta:.2f},$' + \
rf' $\phi_0 = {phi_0:.2f},$' + \
rf' $\dot\phi_0 = {phi_dot_0:.2f}$' + \
'\n' # \n means a new line (adds some space here)
fig.suptitle(overall_title, va='baseline')
# plot 1a: plot from t=0 to t=10
ax_1a = fig.add_subplot(4,2,1)
start, stop = start_stop_indices(t_pts, 0., 10.)
plot_y_vs_x(t_pts[start : stop], phi_1[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
ax=ax_1a)
ax_1a.set_ylim(-3, 3.5)
ax_1a.axhline(y=0., color='black', alpha=0.5)
textstr = r'$\gamma = 1.060$' + '\n' + r' Period 1'
ax_1a.text(-5.8, 0., textstr, bbox=box_props)
# plot 1b: plot from t=28 to t=40 blown up
ax_1b = fig.add_subplot(4,2,2)
start, stop = start_stop_indices(t_pts, 28., 40.)
plot_y_vs_x(t_pts[start : stop], phi_1[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=rf'$\gamma = 1.060$',
ax=ax_1b)
ax_1b.set_ylim(-2.5, -1.6)
# plot 2a: plot from t=0 to t=10
ax_2a = fig.add_subplot(4,2,3)
start, stop = start_stop_indices(t_pts, 0., 10.)
plot_y_vs_x(t_pts[start : stop], phi_2[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
ax=ax_2a)
ax_2a.set_ylim(-3, 3.5)
ax_2a.axhline(y=0., color='black', alpha=0.5)
textstr = r'$\gamma = 1.078$' + '\n' + r' Period 2'
ax_2a.text(-5.8, 0., textstr, bbox=box_props)
# plot 2b: plot from t=28 to t=40 blown up
ax_2b = fig.add_subplot(4,2,4)
start, stop = start_stop_indices(t_pts, 28., 40.)
plot_y_vs_x(t_pts[start : stop], phi_2[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=rf'$\gamma = 1.078$',
ax=ax_2b)
ax_2b.set_ylim(-2.5, -1.6)
# plot 3a: plot from t=0 to t=10
ax_3a = fig.add_subplot(4,2,5)
start, stop = start_stop_indices(t_pts, 0., 10.)
plot_y_vs_x(t_pts[start : stop], phi_3[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
ax=ax_3a)
ax_3a.set_ylim(-3, 3.5)
ax_3a.axhline(y=0., color='black', alpha=0.5)
textstr = r'$\gamma = 1.081$' + '\n' + r' Period 4'
ax_3a.text(-5.8, 0., textstr, bbox=box_props)
# plot 3b: plot from t=28 to t=40 blown up
ax_3b = fig.add_subplot(4,2,6)
start, stop = start_stop_indices(t_pts, 28., 40.)
plot_y_vs_x(t_pts[start : stop], phi_3[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
ax=ax_3b)
ax_3b.set_ylim(-2.5, -1.6)
# plot 4a: plot from t=0 to t=10
ax_4a = fig.add_subplot(4,2,7)
start, stop = start_stop_indices(t_pts, 0., 10.)
plot_y_vs_x(t_pts[start : stop], phi_4[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
ax=ax_4a)
ax_4a.set_ylim(-3, 3.5)
ax_4a.axhline(y=0., color='black', alpha=0.5)
textstr = r'$\gamma = 1.0826$' + '\n' + r' Period 8'
ax_4a.text(-5.8, 0., textstr, bbox=box_props)
# plot 4b: plot from t=28 to t=40 blown up
ax_4b = fig.add_subplot(4,2,8)
start, stop = start_stop_indices(t_pts, 28., 40.)
plot_y_vs_x(t_pts[start : stop], phi_4[start : stop],
axis_labels=phi_vs_time_labels,
color='blue',
label=None,
ax=ax_4b)
ax_4b.set_ylim(-2.5, -1.6)
fig.tight_layout()
fig.savefig('Figure_12.8.png', bbox_inches='tight') # always bbox_inches='tight'